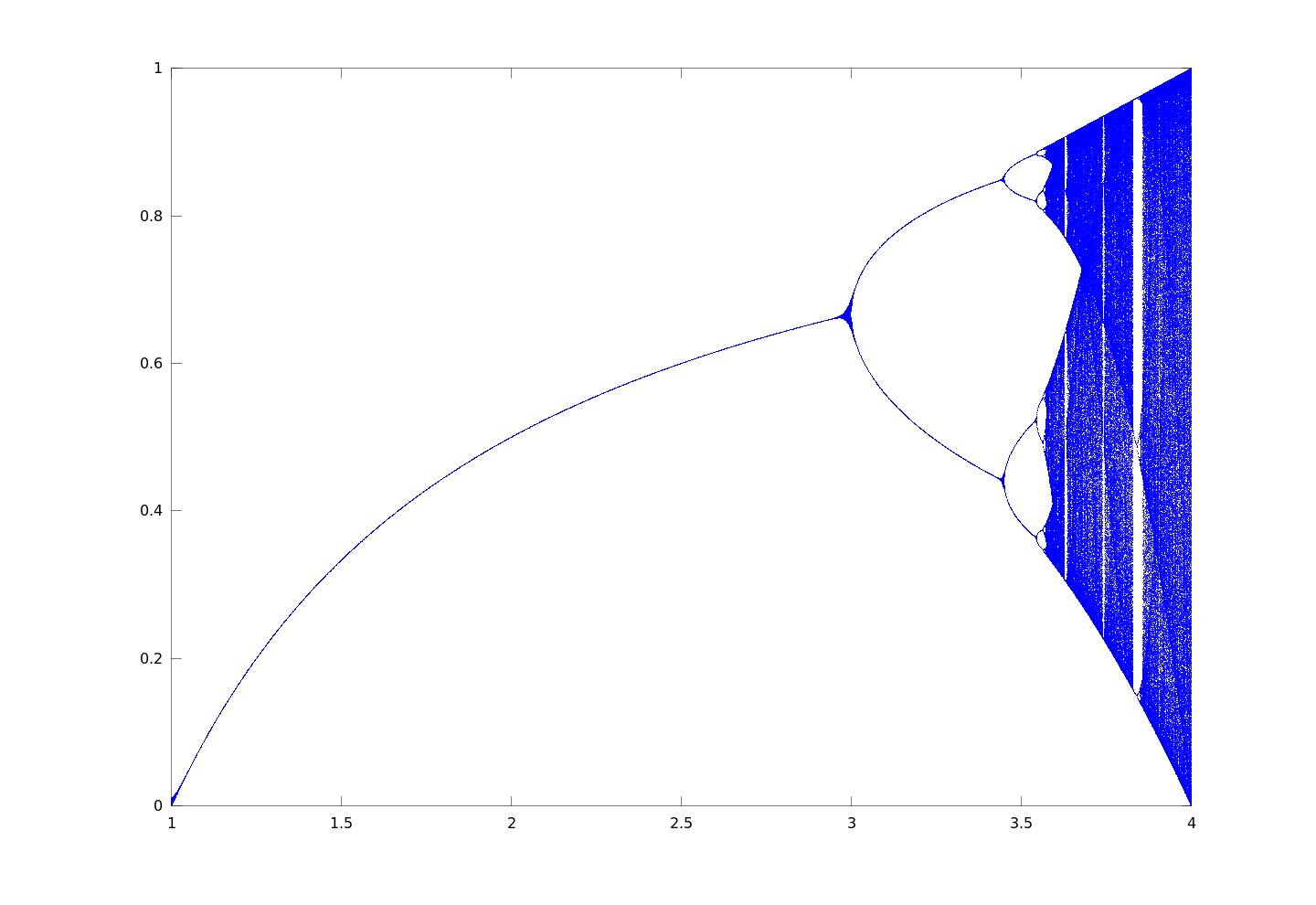
Diagrama de Bifurcação do Mapa Logístico

Ontem, desenvolvi em Octave (alternativa ao Matlab) uma rotina que desenha o diagrama de bifurcação do mapa logístico.

Em posts anteriores já falei um pouco sobre o mapa logístico, um sistema caótico que é muito estudado em grande parte por sua extrema simplicidade:

$$x_{n+1} = x_n r (1 - x_n)$$

O diagrama de bifurcação representa quais os possíveis valores de x (eixo vertical) para cada valor de r (eixo horizontal), desconsiderando as primeiras iterações (o período transiente). Ou seja, para saber quais os possíveis valores de x para r = 3.5, por exemplo, trace uma linha imaginária vertical sobre o ponto r = 3.5 (eixo horizontal) e veja quais pontos de x (eixo vertical) a reta corta.

Perceba que conforme se aumenta o valor de r, o número de possíveis valores de x dobra, até que, para valores de r mais próximos de 4, uma infinidade de valores existem, adquirindo, assim, comportamento caótico naquela região. Segue o diagrama:

Código da rotina:

clear all
X = [];
x0 = 0.6;
r_min = 1;
r_max = 4;
dr = 0.001;
n = (r_max - r_min)/dr;
for r=r_min:dr:r_max
    r   
    x = [ x0 ];
    for i=1:1000
        next_x = r*x(end)*(1-x(end));
        x = [ x next_x ];
    end
    X = [ X ; x(100:end) ];
end
hold on
for i=1:n
    r = r_min + dr*(i-1)
    x = X(i, :);
    plot(x.*0+r, x, '.');
end
hold off
pause